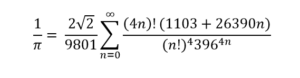‘The Man Who Knew Infinity’
In January 1916, Srinivasa Ramanujan (1887-1920), a self-taught mathematician working as a clerk in Madras, sent a letter to G.H. Hardy (1877-1947), one of the most famous English mathematicians of the day. Ramanujan sent letters to two others but they dismissed them as the work of a crank. This was Hardy’s initial impression but, on closer inspection, he was convinced the mathematics contained in the letter was the work of an unknown but brilliant thinker.
Ramanujan (pronounced Ra-man-ujan) claimed to have discovered a formula to calculate the number of primes below any given number. This was the central problem of contemporary number theory. Unfortunately, Ramanujan didn’t include the formula but there was sufficient other material to convince Hardy of Ramanujan’s brilliance. He was determined to get Ramanujan to come to Cambridge University. Bertrand Russell wrote at the time “In the hall I found Hardy and Littlewood[1] in a state of wild excitement because they believe they have discovered a second Newton, a Hindu clerk in Madras on £20 a year”.
Srinivasa Ramanujan came from a very poor background. He is supposed to have written his mathematics using chalk on flagstones as he couldn’t afford paper. By the age of 13 he was already proving theorems of his own and re-discovering others including eix = cosx + i sinx (which becomes ‘the most beautiful equation in mathematics’, eiπ + 1 = 0, when x = π). Ramuanujan was devastated to find out that Euler had discovered this over 200 years earlier.
He and his family were strict Hindus and Ramanujan believed that he received his ideas from the family’s goddess Namagiri, consort of Lord Narasimha, the lion-faced, fourth incantation of Vishnu. It was only when Ramanujan dreamt that Namagiri commanded him to cross the seas, that he was persuaded to leave India.
H. Hardy was completely different. He was an atheist and had a fear of mechanical tools, never wearing a watch and loathing the telephone. He was unemotional and committed to rigorous proof. For Ramanujan, all that mattered was intuition and evidence. Hardy was quite witty and once told Bertrand Russell: “If I could prove by logic that you would die in five minutes, I should be sorry you were going to die, but my sorrow would be very much mitigated by pleasure in the proof”.
Ramanujan was interested in the study of partitions: the number of ways you can write a number as the sum of other positive numbers. For example, the number 4 has five possibilities: 1+1+1+1, 1+1+2, 2+2, 3+1, 4 so p(4)=5. You would think this was a simple situation with an equally simple formula to calculate p(n). The sequence goes 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101… Mathematicians had searched for centuries to find a formula. The Hardy-Ramanujan formula gives an approximation:
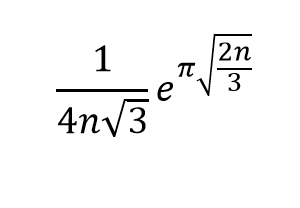 This formula, they showed, gets increasingly accurate as it gets larger. They also produced a formula for the exact number but it is too large to present here! Like all mathematicians, Ramanujan was fascinated by prime numbers. He devised many series approximations for pi, including this one:
This formula, they showed, gets increasingly accurate as it gets larger. They also produced a formula for the exact number but it is too large to present here! Like all mathematicians, Ramanujan was fascinated by prime numbers. He devised many series approximations for pi, including this one:
Even with n=0, this gives pi accurate to 6 decimal places. For each increase in the value of n, roughly eight new digits of accuracy are created.
Ramanujan found life in England hard. He was used to the warmth of southern India, hated wearing shoes and struggled to follow his strict Hindu diet. He was a pacifist during the First World War and he may also have contracted tuberculosis. In 1917, he tried to commit suicide by throwing himself under a London Tube train. Luckily the guard managed to stop the train in time but attempting suicide was illegal then and he only escaped going to prison by being confined to a sanatorium. It was during this time, when Hardy came to visit him, that the famous story of the taxi cab number originated. Struggling to make conversation, Hardy commented that the cab number was rather dull: 1729. Even on his sickbed, Ramanujan quickly protested that this was not the case: 1729 was the smallest number that can be expressed as the sum of two cubes in two different ways[2].
Ramanujan returned to India but died shortly afterwards, aged only 32. He left many notebooks crammed with his idiosyncratic style of mathematics. In one there is a table detailing the number of primes below 100 million. They are very close to being correct and are more accurate than the formula Ramanujan wrote about to Hardy originally. There is speculation that he might have discovered a new formula. In 1976 a lost notebook of his was found and mathematicians continue to study this and his other books. Maybe somewhere in Madras or the archives of Cambridge further work of Ramanujan is yet to be found.
[1] J E Littlewood who worked closely with Hardy for many years.
[2] 1729 = 13 + 123 = 103 + 93