Leonardo Fibonacci lived in the 12th and 13th century and was considered the greatest western mathematician of the Middle Ages. He helped to replace Roman numerals with the Arabic ones we know today but his most famous legacy is the Fibonacci Series, a number sequence from which comes a number known variously as the Golden Mean, the Golden Number or the Golden Ratio which mirrors the proportion seen in nature and perceived beauty. In this series of activities, pupils will investigate the sequence and see how the numbers discovered can be found in nature.
Activity One: Number Patterns
Suitable for: Rec to Year 6
Learning Focus:
- Understand that patterns in number sequences can help us find other numbers in the series
- Be able to calculate terms in a sequence based on information given
Give the pupils simple number sequences (difficulty dependent on age and ability) and ask them to say which numbers come next and why.
1, 3, 6, 10, 15, …
Here, they should spot that the difference between the numbers in the sequence rises by one each time so the next numbers should be +6 to make 21 then +7 to make 28.
The Fibonacci series is different, interesting but not hard to identify if the pupils look closely enough . . .
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,
As you see, the number is the sum of the previous two so ask the pupils what they think the next two numbers might be (paper might be required here!)
As an extension activity, ask the pupils to use a calculator to find the answer to a number divided by the previous one. Try several and they should find similar answers which are known as the golden number of the golden ratio.
Activity Two: Fibonacci in art – drawing faces
Suitable for: Year 1 to Year 6
Learning Focus:
- To be able to draw faces using proportions found from using the Fibonacci sequence
Drawing a face and getting the proportions right with the positions of eyes, nose and mouth is difficult until you use the golden ratio and golden rectangles.
The face can almost always be drawn inside a golden rectangle where the ratio of the height to the width is 1.618 to 1.
Divide this rectangle in half horizontally and you’ll have the line of the eyes.
Draw a vertical line bisecting the bottom rectangle and then draw a rectangle at the top of each half where the position of the bottom line is half the height of the face divided by 1.618. This gives the position of the mouth. To get the position and size of the nose, draw a rectangle from level with the eyes, down to just above the mouth with the width at a ratio of 1:1.618 of the height. Draw the nose in and you’ll have fairly accurate positions of the main facial features, ready to add detail.
Activity Three: Drawing spirals from nature using Fibonacci
Suitable for: Rec to Year 6
Learning Focus:
- To be able to use the Golden Ratio from the Fibonacci series to draw spirals seen in nature
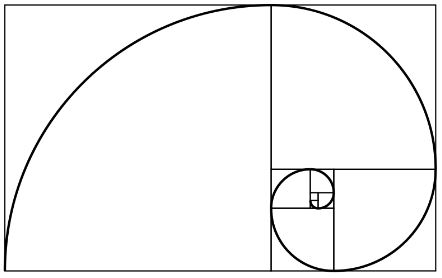
To draw a perfect natural spiral such as those seen in shells, use the following process:
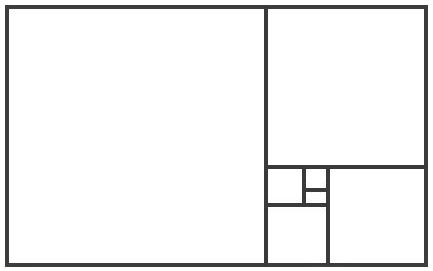
Draw a square. Now draw another square alongside it where the length of the square is a ratio of 1:1.618 of the original square’s size.
From this shape, draw curves which join to form a spiral:
Activity Four: Fibonacci in flowers
Suitable for: Year 2 to Year 6
Learning Focus:
- Investigate the number of petals in different types of flower
- Reason why the number of petals on flowers are numbers in the Fibonacci series
This is an interesting investigation. You won’t find many flowers in bloom on Fibonacci Day so bring in a selection from a supermarket or florists. Ask the pupils to carefully pull the petals off and count how many there were. It doesn’t matter how many you try or which species, they will always find a similar set of numbers which a bright spark will notice are numbers in the Fibonacci series.
Can they decide on a reason why?