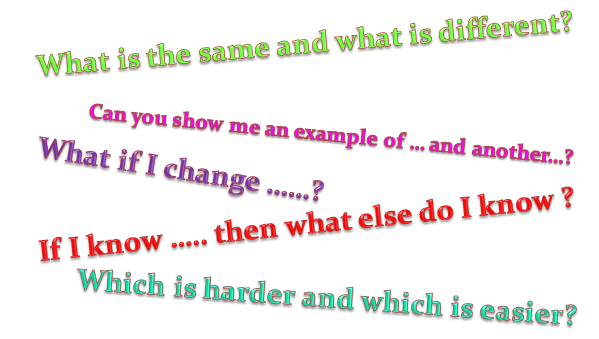The 2014 National Curriculum for mathematics has three main aims- it seeks to enable pupils to develop fluency, problem solving and reasoning in mathematics. I work in a relatively large local authority, supporting teachers of mathematics to improve outcomes for pupils, amongst other things. Following the 2016 end of Key Stage 2 tests, there was much discussion around the disparity of outcomes for many pupils. Whilst some pupils were relatively successful with the arithmetic paper, they did not do so well with the two parallel reasoning papers. In this blog, I offer some thoughts on how we might enhance the teaching and learning of reasoning and problem solving through insightful questioning. The ideas are not exclusively my own, but rather a collection of sources that grew my thinking over time.
It seemed that when pupils were being asked to reason, they were often ‘put on the spot’ with questions such as ‘why?’, ‘can you explain what you have done?’ and ‘can you write a sentence down to show me how you did this?’. All very valid questions, but rather brutal in some ways. For the pupil, questions such as these are almost impossible to answer without good quality discussions to develop language and model thinking. Often, limited time is given for pupils to truly make sense of the mathematics. For the teacher, the need to provide written evidence of pupils’ reasoning can be very frustrating for a variety of reasons.
I offer five key questions that have been developed over time with groups of teachers in the context of my work in schools. They are not intended to be sold as original or as a script, but rather a starting point to encourage mathematical discourse in the classroom. They are:
- What is the same and what is different?
- Can you give me an example of… and another…. and another?
- Which is harder and which is easier?
- What if I change…?
- If I know this, then what else do I know?
Looking at Bloom’s hierarchy with these questions in mind, you may well see opportunities for all levels of thinking skills to be developed with this set of questions.
Teacher colleagues have been very creative with the five key questions. Some have put them at the top of lesson planners so that they focus on using them during teaching and some have shared them with pupils in the front of books, on prompt cards and on working walls. Colleagues have used them during formative verbal and written feedback and with small group problem solving activities. In addition to this, they are useful when engaging in assessment activities or diagnostic assessment tasks with individual pupils since asking the right question at the right time can bring out misconceptions very effectively.
There are many lists of questions available, and many questions you could add to my five, but the idea here was to keep it simple and visible during 
teaching and learning sessions. In this way, colleagues hoped to embed questioning into practice, not only with teachers, but also with pupils. When a child asks the question ‘What if I change that 8 to a 7? I wonder what will stay the same and what will be different?, we know that we are beginning to nurture the mathematical curiosity needed to enable reasoning and problem solving in the classroom and , more importantly, we are beginning to enable our pupils to make sense of the mathematics in greater depth.
My ideas came originally from a great book called ‘Thinkers’ by Bills, Bills, Watson and Mason. Since then, I have dipped into Nrich (a super article by Jennie Pennant on Reasoning) and the NCETM vast range of resources. For those who know and love these questions, my apologies if I have not given appropriate credit where it is due. The desire is to improve mathematics teaching and learning for all and I hope this blog is taken in that spirit.
I include a template for copying onto A4, in order to make double sided A5 cards, for example. Enjoy.
Jo Lees, April 2017
To find out more about mastery and to discover whole-class resources that will assist you in teaching with a mastery approach, visit our maths mastery website: www.collins.co.uk/MathsMastery
