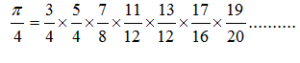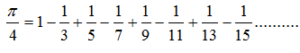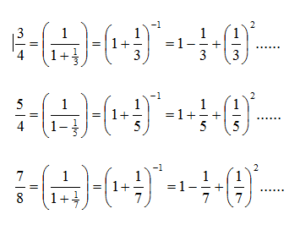We celebrate Pi day on March 14th as this date (3/14) in the American system gives the well known approximation to Pi of 3.14. π is a fantastically surprising number offering both the professional and amateur mathematician a feast of discovery opportunities. Let us remind ourselves of the definition of π, as the ratio of the circumference (C) of a circle to its diameter (d).
π = C/d
The position of the digits of π are precisely determined, therefore in the strict sense the number cannot be random. For example the second decimal place is 4, so you cannot ask a probability question about what is the chance a 7 would occur in this position, but mathematics can ask the related question of ‘is π normal’?
A decimal number is said to be normal when every sequence of n digits is equally likely to occur. By looking at the digits of π and applying statistical tests you can try to determine if π is normal. From the tests performed so far it is still an open question to whether π is normal or not.
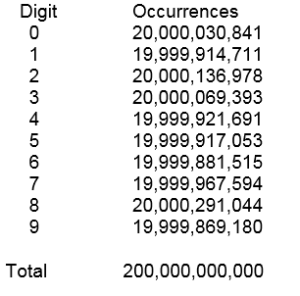
For example in October 1999, Yasumasa Kanada published the distribution of the number of times different digits appear in the first 200 billion digits of π
The digits seem to be fairing evenly distributed with a slight bias towards the number 8. The π test produces a probability of 55% for randomness of this distribution which is statistically insignificant.
We need to remember this surprising fact that if π was normal then all finite blocks of digits could be found in π. For example at position 768 in the digits there are six 9s in succession. The chance of this happening if π is normal and every sequence of n digits is equally likely to occur, is 0.08% This block of nines is famously called the “Feynman Point” after the Nobel Prize winner Richard Feynman. As he once joking claimed that if he had to recite π digits he would name them up to this point and then say “and so on”.
Other special sequences of digits have also been found. At position 17,387,594,880 you find the sequence 0123456789 and surprisingly earlier at position sixty you find these ten digits in a scrambled order. As shown below I have set out the digits in blocks of ten in order to easily see this pattern.
π -hunters search for dates of birth and other significant personal numbers in π asking the question “Where do I occur in the π digits?” If you want to test to see where your ‘special numbers’ are in π, then you can do so by using the free online software called Pi birthdays.
Leonhard Euler was a Swiss mathematician of the 18th Century. His mathematical work was very diverse and he created some beautiful mathematical surprises. He created this formula for π
Euler, 1738
You will notice that the numerator of the fractions is always a prime number. In fact the numerators in this infinite series are all the odd prime numbers!
Euler created this formula by expressing Leibniz’s infinite series in this new form. Here is Leibniz formula for π
Leibniz, 1674
Euler’s proof of his variation of Leibniz formula is very ingenious as it involves looking at the individual expansions of the fractions in his infinite series using the Binomial. Here are the first three fractions to help you see how he constructed the proof.
As all odd numbers can be generated from odd primes his result follows. Up until 1995 a XXX-hunter’s quest was to find more and more digits. To do this a ‘hunter’ had to start from the beginning and calculate all the digits, which came before the new digit they were trying to find.
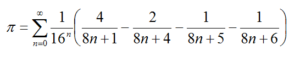Bailey, Borwein and Plouffe, 1995
In this new formula (shown above) any digit can be determined without having to calculate all the previous digits. π is the key term in the denominator of this formula as it allows the calculation of any digit of π in base 16. The quest now for XXX-hunters is to see if it is possible to find a similar formula to calculate the decimal digits of π.
Approximations for Pi abound. Looking back in time the Bible quotes π=3 in ‘Kings 7:23’ and again using the same words in ‘2 Chronicles 4:2’ – “and he made a molten sea of ten cubits from brim to brim….., and a line of 30 cubits did compass it round about.”
Therefore according to the Bible, thirty cubits round about and 10 cubits wide gives Pi as 3. If this were true then all circles would be hexagons! Surprising but true.
π was initially approximated by the fraction 22/7 or 3 1/7 by the Greek mathematician Archimedes around 250BC. This approximation was in common use in schools and in the work place until calculators started displaying a Pi button.
Here are some other approximations for π from history:
- In 1000 BC the Babylonians used 3 1/8
- In 480 AD the Chinese used 355 /113, which is correct to 6 decimal places.
- From the 16th to 19th Century approximations gradually improved giving fractions such as:
- 5419351 / 1725033 correct to 12 decimal places
- 21053343141 / 6701487259 correct to 21 decimal places
You may ask why do we need such a good approximation for Pi, as for most practical calculations 10 or even fewer digits are generally sufficient. For example 39 digits of Pi are sufficient to calculate the volume of the universe to the nearest atom! However, one practical use for the billions of decimal digits of Pi, which have been found, is in testing computer systems to find errors when new programs are being created.
So how can one celebrate Pi day? Well, you could always calculate Pi in some weird and wonderful way on the day. Here are a couple of video examples of how people have done this in the past to help give you some inspiration.
In this first video Matt Parker uses hundreds of pies.
In this second video on Teachers TV, Pi is calculated using French loaves on the streets. This practical video demonstrates the ‘Buffon Needle’ experiment.
Enjoy your Pi parties!
Steve Humble MBE
