Learning Focus: To be able to develop, practise and use alternative strategies for solving mental arithmetic problems
Mental arithmetic is a tricky topic and is one of the biggest causes of distress amongst pupils. Being given five seconds to come up with increasingly more difficult questions is hard enough under any circumstance but in the strict regime of a proper test, it’s a wonder they fare as well as they do.
There are plenty of ways to help overcome the stress but the best one by far is good preparation – it’s just that in the confines of the curriculum, there’s often too little time to be able to spend a lesson a week dissecting the nuances of mental calculation.
My mantra for pupils’ progress is this; it doesn’t matter what score you get as long as you try to get at least one more than the previous test and to do that, they’ve got to choose one question they got wrong and listen carefully to the explanation, practising it at home ready to get it right next time.
As with all maths, there’s not one set way to do many of the topics and giving pupils a range of strategies to choose from is a wise idea. Don’t force them to do what all the others do, instead, let them practise all the strategies and then choose the one that gets the answer correct by the quickest and easiest route for them.
Here are some ideas to share with them…
a) Multiplying by Multiples of Ten
Using the example 63 x 30, one quick and easy strategy is to break down the 30 into 3 x 10 and then do 63 x 3 x 10. 63 x 3 isn’t too onerous – just double it and add 63 so 126 + 63 = 189 and just add a zero for the x10 (but don’t tell the purists I said so!) Answer 1890.
b) Multiplying Big Numbers by Eleven
There’s a dead easy way of doing this too. Using the example 523 x 11, write 523 twice, one under the other with the second time offset by one place to the right then add…
523
523
5753
c) Doubling
The easiest way to double is to break the number into hundreds, tens and units and double each part before adding. So…
Double 163 = double 100, double 60 and double 3…200+120+6 = 326
d) Halving
A similar approach works here but try to break the number down so the hundreds, and tens have an even first digit or 1 as the first digit…
Half of 374 = Half of 200 + half of 100 + half of 60 + half of 10 + half of 4
So… 100 + 50 + 30 + 5 + 2 = 187
e) Adding Sequential Numbers
Pairs of end numbers in a sequence with an even number of elements always add up to the same number, making adding long lists of them easy…
Add 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
5 + 14 = 19 so does 6 +13 and 7 + 12 and 8 + 11 and 9 + 10 giving you 5 lots of 19, so 19 x 5 = 95. If that sum is a little tricky, go for near multiples of ten to solve so 20 x 5 = 100 then subtract 1 x 5 giving 95.
f) Multiplying Near Multiples of Ten
Dead easy again…
38 x 7… think of it as 40 x 7 where you have 7 lots of two, too much! Using the earlier example, do 4 x 7 x 10 and get 280 then subtract the 7 x 2 (14) giving 266.
g) Multiplying Decimals
Here, count up the number of decimal places in the question, ignore them and do a standard multiplication and then put the number of decimal places back in the answer – be careful when the answer has a zero on the end!
e.g. 0.3 x 0.7 count two decimal places then do 3 x 7 = 21 and put the decimal places back so; 0.21
e.g. 0.45 x 0.6 count three decimal places then do
45 x 6 = 90 x 3 = 9 x 3 x 10 = 270 and put the decimal places back so; 0.270 or properly, 0.27
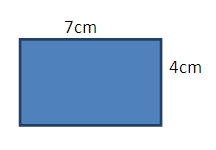
h) Calculating Perimeter
Dead easy this one… add the two measurements given and double them – don’t forget perimeter is a measure of length so no ‘squared’
e.g.