Many adults confess to having difficulties in Maths at school:
“I was an extremely poor pupil in arithmetic and algebra, and still have great difficulty with the abstractions of numbers and letters. I am slightly better at solid geometry because it appealed to my imagination, but even in that subject I never excelled at school.”
This was Maurits Cornelius Escher recalling his school years. His work is familiar to many Maths teachers but few are aware of the mathematical research he carried out.
He was born 115 years ago, on 17th June 1898. He studied as an architect but soon switched to graphic arts.
After his studies in 1922, he travelled for most of a year throughout Italy and Spain. During this time he went to the 14th century Alhambra Palace in Granada, Spain. The palace is decorated with highly geometric tiles.
The Moors who built the Palace believed that only God could create living things and that it was a sin to represent them – hence the geometry. Escher found the tiles a rich source of inspiration. He returned again in 1936 paying his fare there with prints from his sketches. Escher became obsessed with tiling patterns that filled the plane. Unlike the geometrical shapes used at the Alhambra, Escher used animal motifs both real and phatasmic.
In 1937, Escher showed his sketches to his half-brother, a professor of geology, who immediately recognised that the periodic patterns would be of interest to crystallographers. His brother sent some technical papers to Maurits, including one by George Pólya (1887-1985), analysing crystal symmetry. In particular, Pólya classified the 17 periodic planar tilings. It is reputed that the Alhambra Palace has all 17 possible tilings (I only found 15 when I visited a few years ago).
Escher based some of his drawings on this classification, such as Development I, which has four interlocked, rotated lizards slowly morped into squares.
For the next 4 years Escher devoted himself to a methodical investigation of the “Regular divisions of the plane into asymmetric congruent polygons” – the title of his private notebook. In 1954 the International Congress of Mathematicians was held in Amsterdam with an exhibit of Escher’s prints. Roger Penrose visited and was fascinated, especially with Relativity, which shows three staircases shown from different viewpoints.
On returning to England, Penrose came up with his famous impossible figure:
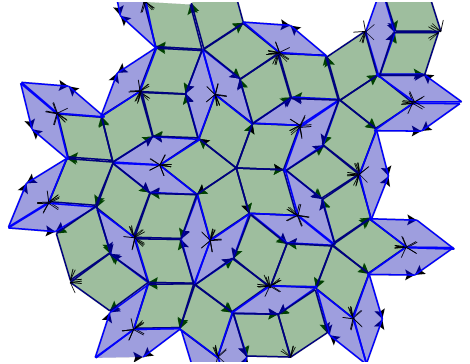
He sent this and other sketches to Escher, who in turn created some of his perpetual motion drawings: Waterfall and Ascending and Descending. Penrose went on to investigate aperiodic tilings (ones with no translational symmetry). It was not known whether such a tiling was possible and, it was only in 1974 that he came up with a pair of polygons that can tessellate aperiodically:
The tiles have to be aligned by matching the arrows.
Why not try creating this tessellation which has no translational symmetry and yet will fill the plane. Alternatively, try making some ‘Escher-type’ tessellations. The classic book “Creating Escher-type Drawings” by Ranucci and Teeters is expensive but the Association of Teachers of Mathematics (www.atm.org.uk/resources) has a free series of booklets on Symmetry by Bob Burn. “Sorting by Symmetry: Patterns over a Plane” includes analyses of Escher tessellations. You never know, doing an end of year project on tilings might not just be a fantastic filler, but might switch on a future Escher!
Don Hoyle
Mathematics Matters
