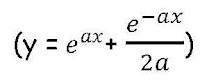Keeping it in the family
It seems to be often the case that mathematical aptitude is not evenly spread in families. Parents often say they can’t help their gifted child at home, as they were rubbish at Maths themselves. There are exceptions and here are some notable ones from the history of Mathematics.
Theon and his daughter Hypatia of Alexandria, lived in the 5th century AD. Theon is famous for his versions of the works of Euclid. In fact, his was the standard version of Euclid’s Elements used for over 1500 years. Euclid’s treatment of geometry fundamentally changed the nature of the subject, making proof central to future mathematics. Hypatia helped her father with this and also wrote versions of the work of Diophantus and Apollonius. She is particularly known for her explanation of the latter’s work on conics. She is also known for the manner of her death – she was killed by a mob of fanatical Christians at a time of political and religious conflict.
Euclid’s Elements was also central to the work of Farkas Bolyai (1775-1856) and his son János (1802-1860). They lived in what is now Romania. Farkas struggled to make a living as a mathematician. He was paid so little as a teacher, he ran the College pub. His main work, Tentamen, was an attempt to give a rigorous and systematic foundation to Mathematics. Euclid had done this for geometry; proving results from basic, self-evident axioms. One of these axioms, the fifth, stood out as it looked like it should be proved from simpler ones. An equivalent of this axiom, called Playfair’s axiom, states that you can draw only one line parallel to another line through a point not on the line.
In 1804, Bolyai thought he had deduced this from the other axioms. He sent this to his life-long friend Gauss, who discovered an error in the work. Farkas attempted to stop his son carrying on with the same work. János explored the geometrical implications of not assuming the fifth postulate was true – this heralded the understanding of non-Euclidean geometries. In Bolyai’s geometry no parallel line can be drawn. Such a geometry is wholly consistent and turns out to be that drawn on a hyperbolic surface (like a saddle). In this geometry the angles of a triangle sum to less than 180º.
The greatest family of mathematicians has to be the Bernoullis. In three successive generations, this family had eight members who made significant contributions during the 18th century. They were a wealthy family of Swiss traders but the two brothers Jacob and Johann resisted their father’s wish that they take over the family spice business and they studied mathematics instead. Jacob invented polar co-ordinates and calculated the value of e. In 1690 he renewed interest in the problem of finding the curve made by a loose chain hung between two points. Amongst those coming up with a solution was his brother Johann, who showed that the curve was a catenary:
where ‘a’ depends on the mass of the chain.
Jacob was also interested in logarithmic spirals. These are sometimes called equiangular as a line from the centre is cut by the curve always at the same angle. He asked that one be included on his grave with the words ‘Eadem mutate resurgo’ (‘Though changed, I shall arise the same’). Unfortunately, the artisan engraved the wrong type – an Archimedean spiral (equal gaps) rather than a logarithmic one.
 |
| The wrong Spiral on Jacob Bernoulli’s plaque |
Of Johann’s sons, Daniel is the most famous for his work on fluid mechanics especially the inverse relationship between the speed and pressure of a fluid – the basis of aeroplane wings.