How do you know? What else can you find?
“Problem solving” has become shorthand for the assessment objectives AO2 and AO3 in the maths GCSE subject content.
One of the best things about the new subject content is the expansion of the section on assessment objectives. Where we used to have three short sentences, we now have fifteen bullet points showing what students should be able to do. It makes it much clearer how to interpret “Reason, interpret and communicate mathematically” and “Solve problems within mathematics and other contexts”.
This can help teachers to review their teaching and consider how well they are meeting the objectives.
Some bullet points are easier than others. “Make deductions and draw conclusions” seems to happen more naturally than “assess the validity of an argument” or “evaluate methods used”.
I would like to present a familiar task and think about how it might be developed to cover some of the more hard-to-hit bullet points.
The task
Think of three consecutive positive whole numbers.
For example: 4, 5 and 6.
Square the middle one. 5² = 25
Multiply the first and last. 4 × 6 = 24
What do you notice?
So we make a prediction and test it a few times.
The proof
Now can we prove it?
A likely method is to call the numbers n, n + 1 and n + 2
Then we compare (n+1)²=n²+2n+1
with n(n+2)=n²+2n
Okay, but could we demonstrate the result in a different way?
We could call the numbers n – 2 , n – 1 and n
Then we compare (n-1)²=n²- 2n+1
with n(n-2)=n² – 2n
Or we could call the numbers n – 1 , n and n + 1
Then we compare n²
with (n-1)(n+1)=n²-1
Is one better that the others?
However instead of algebra, we could take a geometric approach.
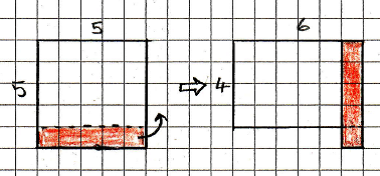
Look at this diagram.
We can “see” that the difference is one.
Is it the same for other sets of numbers? How does this demonstration compare with the algebraic one? Is one more convincing than the other? Is one better than the other? Are two better than one?
Perhaps there are other ways to demonstrate the result?
Some extensions
“What if …?” is a question we should always have in the back of our minds if we are thinking mathematically.
What if the numbers are not consecutive but differ by two?
Here is a picture.
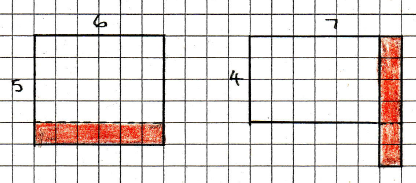
What is happening this time?
Draw another picture. Do some algebra.
What happens if the numbers differ by three? Or four?
Alternatively, let’s go back to the start but this time take four numbers.
Let’s choose 4, 5, 6 and 7.
What can we do with them?
Here is one idea:
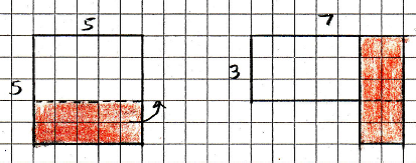
What have we learnt?
The general approach I am suggesting here is in two parts:
- Look for different ways of demonstrating a result and compare them (“Is there another way to show this?”)
- Look for ways of extending a result to give further results (“What if …”)
If you look at the assessment objectives you will see that many aspects of AO2 and AO3 are covered including: present arguments and proofs; assess the validity of an argument; interpret results in the context of a given problem; evaluate methods used and results obtained.
One to try
A standard GCSE result is that the opposite angles of a cyclic quadrilateral add up to 180°.
The usual proof relies on first establishing that the angle at the centre is twice the angle at the circumference and then using that result.
Here is a picture showing that divides a cyclic quadrilateral into four isosceles triangles. O is the centre of the circle.
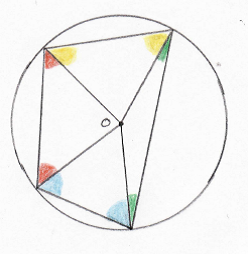
How does this demonstrate the result? Is this more convincing than the usual proof?
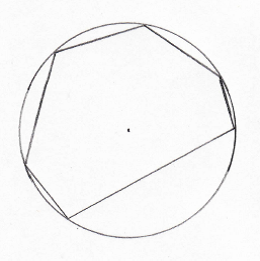
And can we extend the result?
Is there a rule about the opposite angles of a cyclic hexagon?
By: Chris Pearce, author of Collins Maths Skills Builder and New GCSE Maths – Multistep and Problem Solving Skills
Chris has over 30 years’ experience teaching maths in secondary schools. He worked as an adviser with the National Maths Strategy for over five years. He has written a number of textbooks and other maths resources. He has also worked as a consultant in the Middle and Far East.