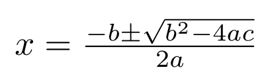Credit where credit is due
Abstract: This article outlines the work of Paolo Ruffini who first gave a proof of the impossibility of an algebraic solution to quintic equations.
This year, 2015, will be the 250th anniversary of the birth of Paolo Ruffini (1765-1822).
You can be excused for not recognising this name! In 1799, he stated that a general algebraic solution could not be found for polynomials axn+bxn-1+cxn-2+…=0 if n>4. He offered a proof but his work was largely ignored at the time. That his proof was over 500 pages in length and hard to follow could be part of the reason for this. More likely it was an unwillingness to accept defeat on what had been a classic problem for mathematics at the time, exercising many of Europe’s eminent scholars such as Euler and Lagrange.
GCSE mathematics includes knowing the general formula for solving any quadratic:
Even the Babylonians knew this result hundreds if not thousands of years before Christ – not in algebra, which hadn’t been invented, but as an algorithm. Early algebraic formulations were developed by the Hindu mathematician Brahmagupta (598-665 AD) and Al-Khwarizmi (c800 AD), who was a member of the “House of Wisdom” in Baghdad. It took until the 16th century before a formula was found for cubics. The story of this is quite fascinating and will feature in a future blog. That every quartic can also be solved algebraically was discovered at the same time. The quartic formula is so complex that it is rarely used. You can imagine that it was a surprising idea that the process of finding general solutions, though increasingly complicated, would stop. Stop it does and there is no general formula for quintics and beyond.
Ruffini was a very talented mathematician. He went to the University of Modena aged 18 and within 4 years, though still a student, he became a lecturer. He was talented as a doctor and at one stage was not only the chair of applied mathematics at the University, but also practical medicine and clinical medicine as well. He sent a copy of the book with his proof to great mathematician Lagrange but didn’t get a reply. He sent another copy saying:
He continued for the rest of his life trying to get feedback on his proof. He finally got some recognition, just before he died, from the French Mathematician Cauchy. His death came from treating patients during a typhoid epidemic. It turns out his proof was incomplete and assumed some unproven results, but Ruffini should, in his 250th anniversary, get some credit for his pioneering work.
Don Hoyle
Mathematics Matters