Take a deck of cards and ask someone to shuffle it thoroughly. With the deck face down, ask them to name any two cards they think might be next to each other, not worrying about which suit, just the name/number.
Before you take a look, ask them what they think the chances are that their two cards will be next to each other in the pack. Now turn over the deck and fan through it. Hey Presto, their named cards will be somewhere right in there next to each other. Or will they?
Well it turns out that it is slightly more likely that you do NOT find the named cards next to each other (50.6 % chance). But only slightly. Surprised? I know, I was when I first discovered this fact.
So what happens if the deck size is reduced? If the deck size is 40 the cards will be ace to 10 inclusive. With a small size deck, such as 16, the cards will include ace to 4 inclusive. But what really matters is that the reduced deck is made up of sets of four cards with the same face value.
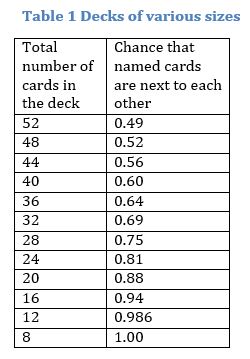
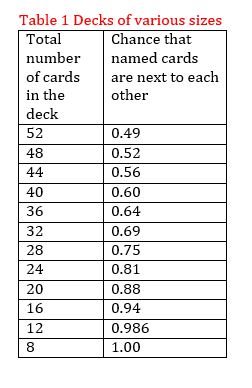
When I ran a simulation for decks of various sizes the following chance of at least one named card pair being next to each other was found (see table 1). For example, when the deck is reduced to 32 cards the chance of the pair of named cards being next to each other at least once is 69%. The only true certainly, of course, is when there are only 8 cards in the deck.
An approximate theory
Say we select Jacks next to Queens. We can work out the chance of this as follows.
Remove the Jacks, shuffle the remaining 48 cards and put them in a row on the table. Suppose that no two Queens are adjacent.
Then put the first Jack to the left, to the right or between two cards that are already on the table. There are 49 possible positions and 8 of them generate a Jack-Queen pair. Thus, the probability that no pair appears in this first move is 41/49.
Similarly, for the second Jack the probability it does not land adjacent to a Queen is 42/50. After four steps we know that the probability of failure in all steps is 41x42x43x44/49x50x51x52=0.5014. Note that if two or more of the Queens are adjacent, the probability is larger. This demonstrates again that the probability this trick is successful is just under 50% at 0.49856, which is very close to the computer simulation result from table 1 of 0.49.
A ‘magic trick’ variation
In this version of the Neighbour Problem you select three cards that you want next to each other. Then look for any two of the three named cards to be next to each other in the deck.
Say you select King, Queen and Jack. In a well-shuffled pack we know from the above that the chance of finding a Queen next to a Jack, or a Jack next to a King, or a King next to a Queen is about 50%. Because three cards have been given as options this increases the chance that at least two of the named cards will be next to each other. As they are not independent events, this suggests (1/2)^3 as the chance NONE of the events happen is 1/8th (12.5%), implying that the chance that at least one of the named sets will occur is just under 90%.
This simple maths magic suggests coincidence happens more than you might imagine.
Written by Steve Humble, Newcastle University