The ‘travelling to relatives’ season is nearly upon us. With this comes the need to pack suitcases and make sure you can fit everything in without leaving any important Christmas items behind. Packing is a very logical mathematical exercise and when packing anything from suitcases, the boot of your car, or to giant transport containers, the golden rule is always to put the largest boxes in first.
The packaging of objects into fixed spaces has been an interest of mathematicians for centuries. The first record of this is in 1606 when the mathematician Johannes Kepler was asked by Sir Walter Raleigh how best to stack cannonballs on the decks of his ships. This branch of mathematics became known as Granular Matter.
Other places that you will find the mathematics of Granular Matter are at fundraising events such as when you’re asked to guess the number of sweets in the jar. The rules are usually very simple. You have one chance to guess and at the end of the day all of the guesses are examined and the winner is the one that is the closest to the number of sweets in the jar. The reward is often the jar of sweets itself. Is there a way you can estimate the correct number of sweets? On a more practical level, an answer to this type of ‘how many’ question would be useful to a chemical engineer when working out the number of plastic pellets in a container, or to a farmer for calculating grain in a silo.
The mathematical understanding of packing objects has been found to be much harder than anyone had anticipated. A greater appreciation of how granular matter moves, twists, spins and breaks, is the key to how major cost savings can be made during the production and packing processes. Yet granular mathematics is still not fully understood and is an area of ongoing research and development.
This whole area of mathematics has many interesting and curious experiments that students can investigate in class. Why not try to perform a Granular Matter packing experiment this Christmas such as the ‘Brazil nut’ effect. All you need is a box of mixed nuts (when has there been a year when you haven’t had one?!). Shake the box from side to side and in time all the Brazil nuts will rise to the top!
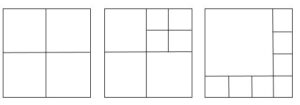
Other interesting packing problems you can explore involve shapes contained inside other shapes. Interestingly a square can always be divided up into an exact number of smaller squares, apart from the cases of 2, 3 or 5 squares. Here are some examples of a square being divided into 4, 7 and 8 squares.
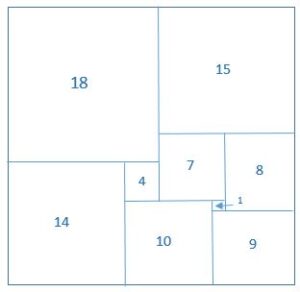
The reason that 2, 3 and 5 are not possible is due to the fact that the four right angles of the initial square must be in the smaller squares and this cannot happen in the three special cases of 2, 3 and 5. ‘Mrs Perkins’s quilt’ is a puzzle version of the square mathematical experiment shown above. The challenge for the quilt puzzle is to find the fewest different sized square pieces required to fill a given square area. There are many ways to solve this puzzle, one solution for the 32 square is given below.
Bill Tutte, who came up with the concept upon which Mrs Perkins’s quilt puzzle is based, was one of the first people to study the mathematics of ‘squaring the square’. He found that as well as being a fun logical challenge it had many applications, such as in the field of electric circuits.
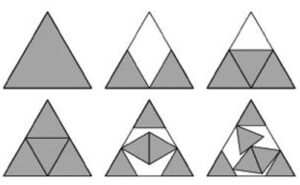
Mrs Perkins’s quilt puzzle looks at packing squares into squares but what about packing other shapes into different spaces? The illustration below shows the first few cases of the best-known ways of packing a set number of same size equilateral triangles into an equilateral triangle.
You can create similar puzzles for different shapes, such as packing a set number of equilateral triangles into a square.
Before I finish let’s return to the initial problem and try to find an approximate method to calculate the number of sweets in a jar.
You can find the volume by multiplying the number along the width and length of the base by the number of sweets in the height of the jar. Granular Matter theory then tells us that on average a jar of mixed shapes will have about a 30% air gap in between the sweets. This percentage value will of course vary depending on the shape of the sweet. For example, an unshaken jar of spherical shaped sweets will have a gap of 39%, but if you gently shake them from side to side a few times this will drop to 35%.
For a jar with 6 sweets along both the width and length of the base and a depth of 15 sweets you would need to calculate 6x6x15=540. Then to take account of the gap in between the sweets, reduce this total by thirty percent 0.70×540 giving an answer of 378 sweets in the jar.
We can now claim the prize and have a tasty Christmas with our sweets!
Steve Humble FIMA
Newcastle University
http://drmaths.org